Shader Performance Improvements in Forge of Empires

With our new underwater era outpost we wanted to add a post-processing effect to simulate the water by adding a small amount of animated visual distortion on top of the rendered game scene.

After some back and forth between the art and dev departments we settled on the following implementation:

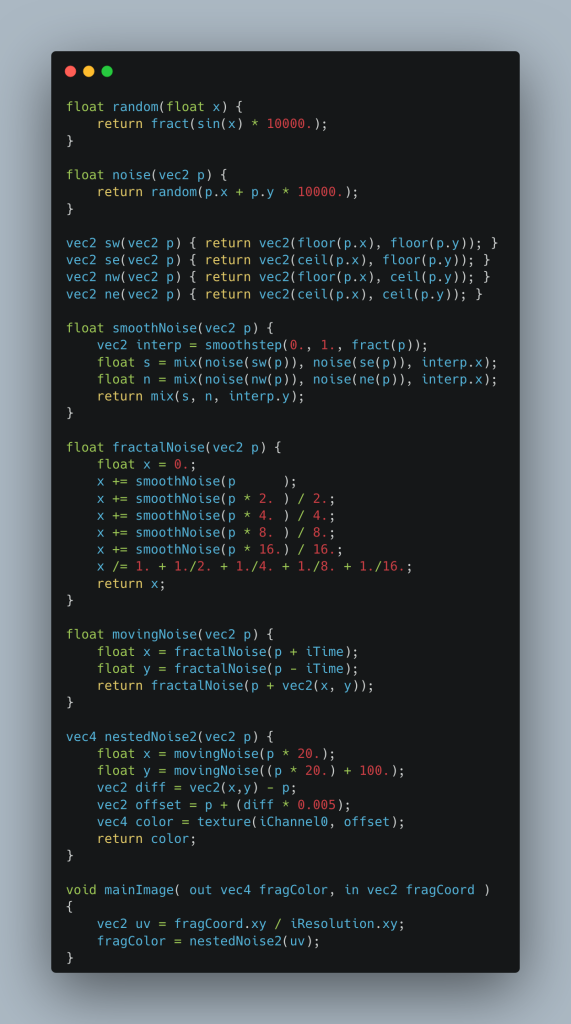
Whilst this produced the intended visual effect and the performance hit on most devices we tested this on was minimal, we also found during testing that on some mobile devices this shader had a really drastic impact on the games framerate (bringing it from our target 30 FPS down to ~5/6 FPS).

To improve the situation we first looked into some automated options, such as this GLSL optimizer originally used by the Unity engine: https://github.com/aras-p/glsl-optimizer
Sadly the “optimized” version of the shader was not only a lot bigger then the original but it also ran a whole order of magnitude slower than the original version.

At this point we looked into what kind of output the optimizer produced and noticed that it’s not really optimizing the code in any way, it simply “unrolls” the entire thing and obfuscates the variable names:

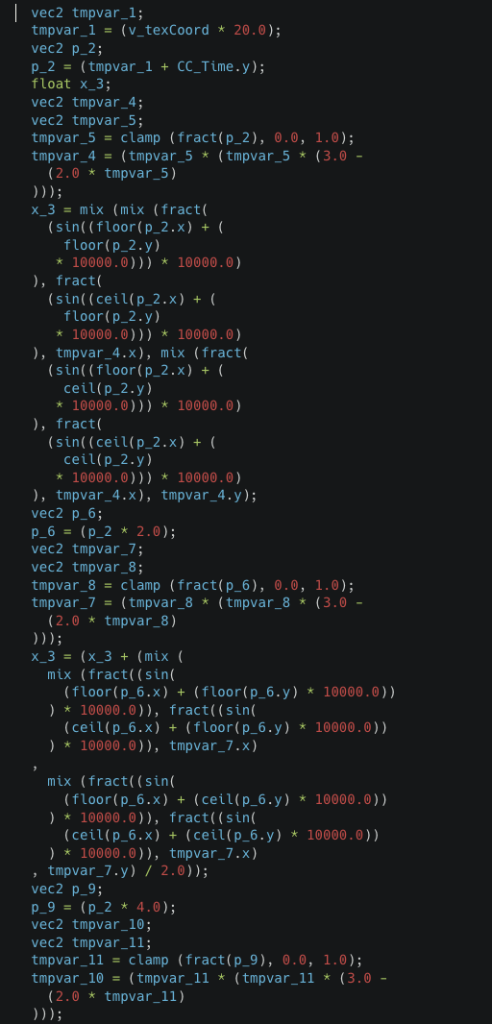
This is only a fraction of the ~700 lines of output from the optimizer. Although this doesn’t actually run faster it does help us identify the performance bottleneck quite easily:
We are calling sin() in this shader 120 times for each fragment, and unfortunately this is extremely slow on some mobile GPUs.
The fact that we call it that many times was not immediately apparent in the original version, as there is only one method with a single call to sin().

At this point it makes sense to look a bit deeper into what this shader is actually doing to achieve the intended effect:
In short the shader is using a form of Fractional Brownian Motion (see https://en.wikipedia.org/wiki/Fractional_Brownian_motion) to offset the read UV coordinates.
The X and Y axis each get their own displacement, which is based on a 2D noise algorithm which in turn combines 5 octaves of noise at different scales to produce a nicely uneven distortion effect.
Reducing the number of octaves would reduce the number of calls to sin() but also immediately changes the visual nature of the effect, so sadly this was not really an option.

At this stage we looked into alternatives for the call to sin() which would perform better on the affected GPUs.
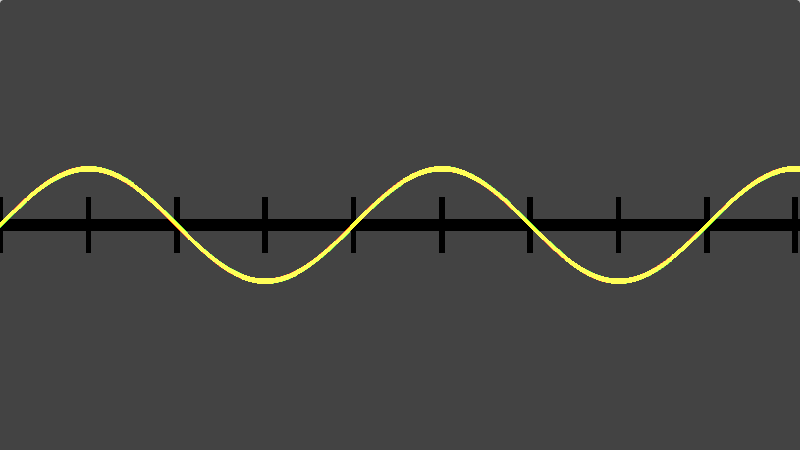
In order to debug this visually we first set up a shader which plots the curve produced by sin():

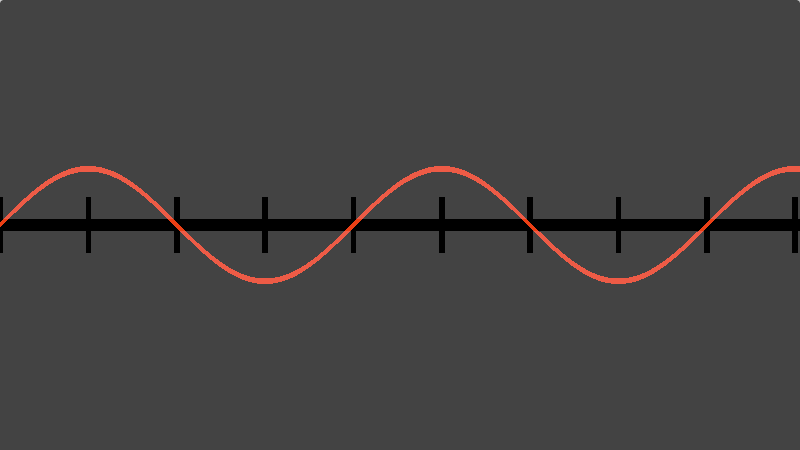
Here the red line is the output of the GLSL sin() call and we will use it as a base to compare against potentially faster approximations.
Then we started looking into a multitude of different ways to get similar output that will match the sin curve.

First up is a triangle wave based approximation (https://en.wikipedia.org/wiki/Triangle_wave):

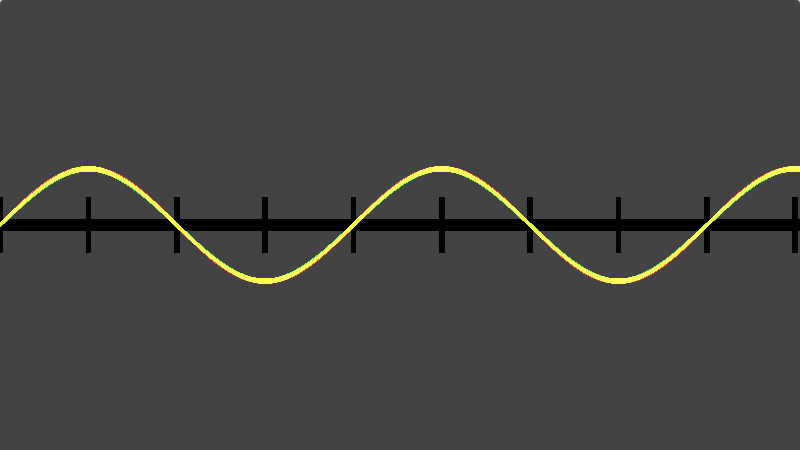
Here the original red line is still included but overlaid on top is the output of the triangle wave method in green.
This allows us to easily see how much error there is in the approximation as Red/Green pixels mean there is a divergence, yellow pixels means the values overlap.
Result: not bad, this comes pretty close to the real values and was slightly faster than the original version on the slow GPUs but sadly the performance gain was too small.

Next up is an approximation using a Taylor Series method (https://en.wikipedia.org/wiki/Taylor_series):

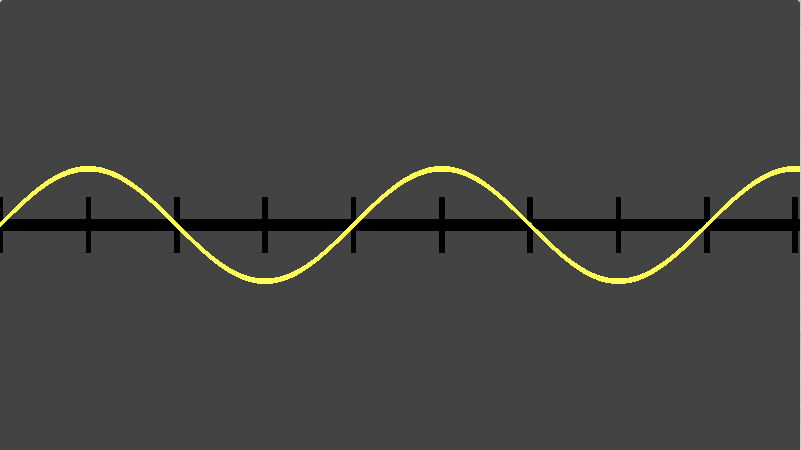
Result: even better than Triangle-Wave in terms of accuracy at about the same performance. Still not fast enough for our use-case though.

This next one is a strange mathematical approximation which I found somewhere online but can no longer find the original source. It seems to be using a parametric curve to approximate the sin curve:

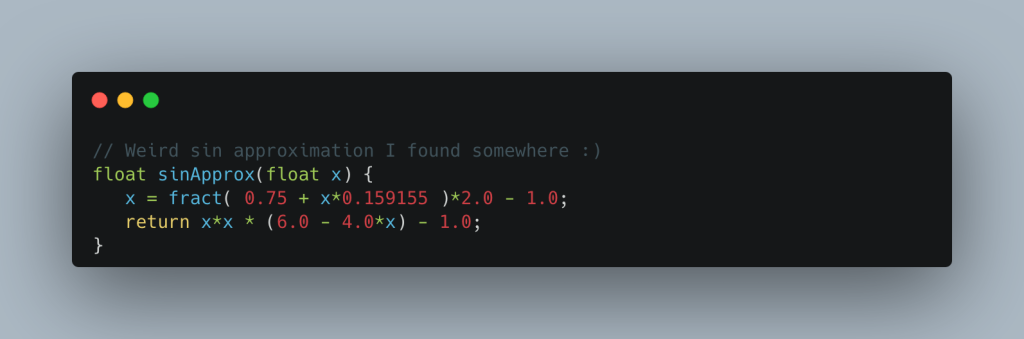
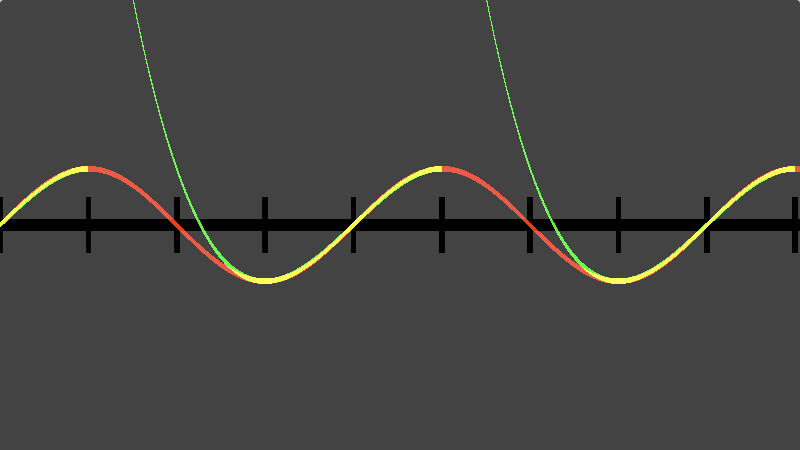
Result: Clearly this fails at values greater than π and smaller than -π but since the curve is symmetrical there are some cases where this could be used as a replacement for sin().

Last in this list is a simple table lookup. Since we don’t care about having super accurate values here we could just hard-code a table of sin values as a constant into the shader and use that for lookups:

For extra precision in this one it would be possible to linearly interpolate between the closest 2 values in the table.
Result: Sadly the lower-end GPUs that this optimization was intended for in the first place also often have hard limits on the sizes of arrays they support, often having a limit well below the 360 values used here making this unusable on those devices.

Throughout this process we also compared what the actual noise output would be using one of these approximations against using the hardware sin() method to ensure we are getting a similar noise and motion over time:

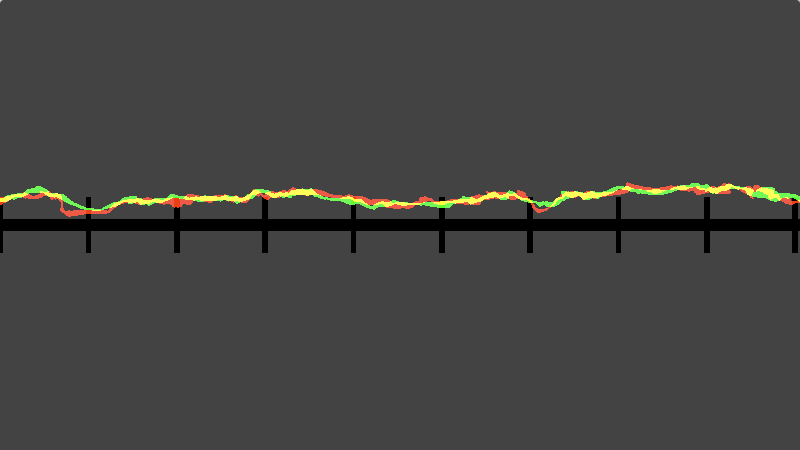
Even though some of these approximations did improve the performance on the slowest devices we tested the actual improvement was nowhere near enough to consider the issue fixed.
At best we got the shader to run about twice as fast, bringing the framerate to somewhere around ~12 FPS but we are still targeting 30 FPS.
At this point the performance improvement gains were shrinking fast and it started to become clear that this approach would not likely lead to a shader with the kind of performance we were expecting so we needed to change direction.

Instead of pushing forward with trying to get the FBM noise to run fast enough on slow GPUs we figured that maybe we can just use a cheaper noise method which still produces a visually pleasant effect.
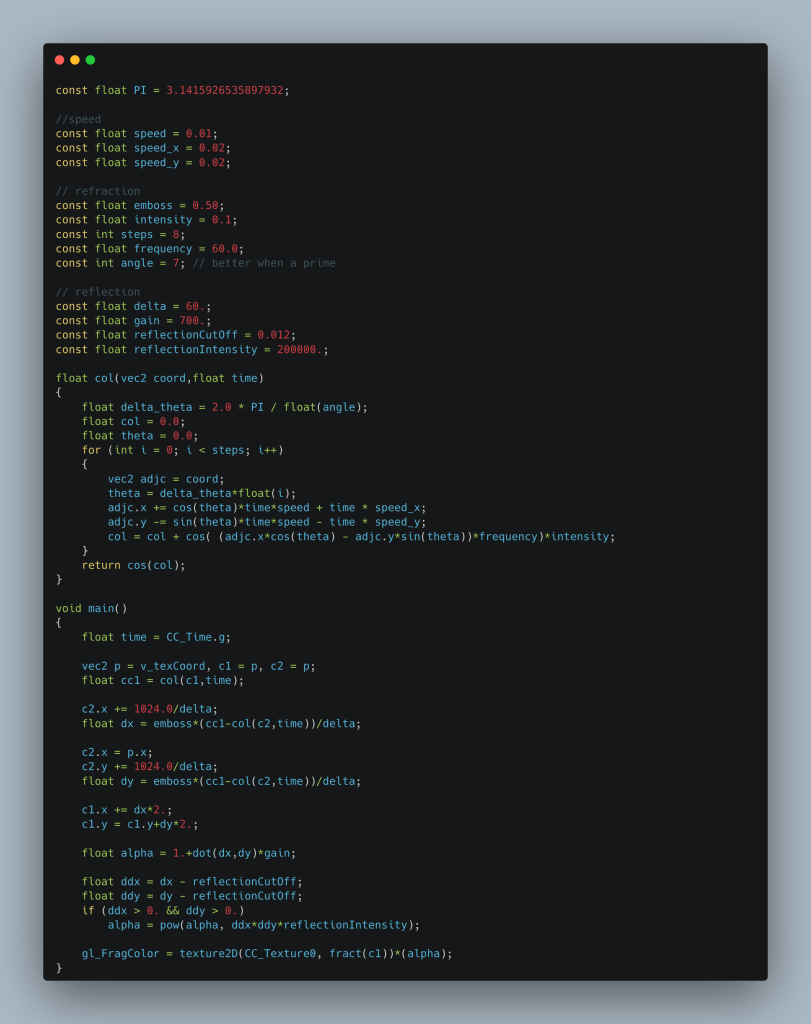
This time we simulate a water surface with displacement and embossing, resulting in an entirely different set of parameters which control the motion and amount of the distortion.
With the right settings this looks very close to the original and even allows us to tweak the appearance of the water in the future – most importantly this one runs smoothly even on weaker mobile GPUs.

Behold, the new water shader:

Ville-Veikko Urrila

Senior Software Developer, Forge of Empires